We all are taught in the schools about different types of shapes. We all might see all these shapes in our daily life as well. The common shapes taught might include circles, triangles, squares, rectangles, etc. Mostly all these shapes have further different types which makes them different because of the singles and angles that they have. In geometry classes, we all are taught about different types of triangles that differ in side length like an equilateral triangle, Isosceles triangle, and scalene triangle.
What are Scalene Triangles, and how do they work?
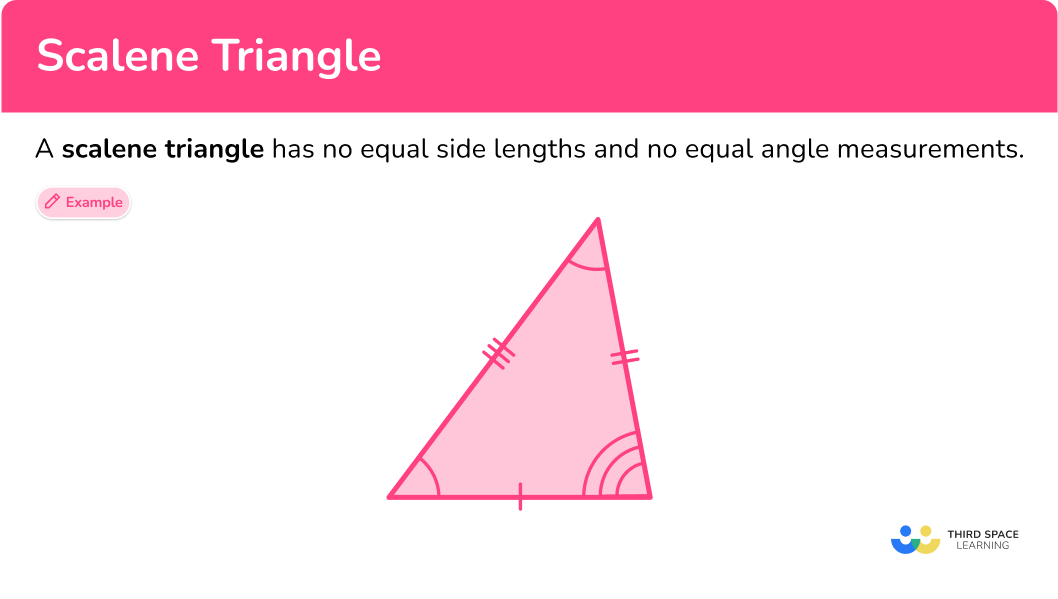
In the equilateral triangle, all sides of the triangles are equal. If AB = 4cm, then BC and CA will also be 4 cm. In the Equilateral triangles, two opposite sides of the triangle will be equal. If PQR is a triangle PQ and PR is 5cm whereas QR is 3 cm. Now the last triangle is the scalene triangle which has no equal sides. If there is a triangle XYZ, so XY is 4 cm, YZ is 8cm and XY is 5 cm. So in this triangle, there will be three different angles.
The scalene triangle is the triangle that has all three sides unequal in length and have different angles. Though the sum of the interior angles comes out to be equal to 180 degrees. So it meets the main property of the triangle that all interior angles sum must be equal to 180 degrees. Even the scalene triangle is classified into further parts. Let’s have a look at them.
- Acute angle triangle: It is the triangle that has all sides unequal so are the interior angles. But all the interior angles are less than 90 degrees. So it qualifies as an acute angle triangle.
- Obtuse angle triangle: It is a triangle with unequal sides and angles but has one angle greater than 90 degrees.
- Right angle triangle: In this type of triangle the scalene triangle has one angle equal to 90 degrees.
So it is better to classify the scalene triangles and know more about them. Here is a list of the properties related to scalene triangles are stated below:
- All sides are unequal
- All angles are unequal
- There is no line symmetry in the triangle
- It has no point symmetry
- The angles in the triangle can be acute, obtuse, and even right angles.
There is a formula to calculate the area of the scalene triangle which is stated as below:
Area of scalene trainable = (1/2) * b * h
Here, b stands for base and h stands for height.
If there are only sides given of the triangle, then there is a requirement to apply Heron’s formula.
For example, PQR is a scalene triangle whose base is 10 cm and height is 8 cm. Find the area of a triangle.
Solution: B of triangle PQR = 10 cm and height = 8 cm
Area of scalene triangle PQR = (1/2) * b * h
= (1/2) * 10 cm * 8 cm
= 9 cm2
To calculate the perimeter of a triangle, the person needs to add all of the lengths of the sides of a triangle. So the formula is
Perimeter = a + b + c units.
For example: If there is a scalene triangle ABC whose sides are AB = 5 cm, BC = 7 cm and CA = 10 cm. Calculate perimeter.
Solutions: AB = 5 cm, BC = 7 cm and CA = 10 cm
Perimeter of triangle ABC = AB + BC+ CA
= 5 cm + 7 cm + 10 cm
= 22 cm
There are a lot of things about the triangle that every person needs to understand properly. This is not all for more information about the concept of different types of triangles, the student or any person can consult the experts at Cuemath. The experts know how to explain the concept to their children so that they can easily grab them and relate the concepts in their real life. The person just simply needs to visit the official website i.e. Cuemath.com for more information about courses.
Also Read:
- Sum of Squares
- Interest Coverage Ratio
- Multinomial Distribution
- Form 2106
- Finance Jobs for 2021
- New Fund Offer (NFO)
- Bearer Bond
- Smurf
Stay tuned to Centralfallout for the latest scoops and updates of Latest News, Trending News, Technology News, World News and Entertainment News.





